Straight Line and a Point

The equation of the perpendicular bisectors of the sides $AB$ and $AC$ of a  $\Delta ABC$ are  $x-y+5=0$  and  $x+2y=0$  respectively. If the point $A$ is  $\left(1,-2\right),$ then the equation of the line $BC$ is.

Two mutually perpendicular straight lines through the origin form an isosceles triangle with the line $2x+y=5$, then the area (in sq. units) of the triangle is

If a point $\left(a, a\right)$ falls between the lines $|x+y|=4,$ then

If $m$ and $n$ are the lengths of the perpendicular from the origin to the straight lines whose equations are $x\cot \theta -y=2\cos \theta$ and $4x+3y=-\sqrt{5}\cos 2\theta$ $(\theta \in (0,\pi \left)\right),$ respectively, then the value of $m^2+5n^2$ is

If the points $\left(x,-3x\right)$ and $\left(3,4\right)$ lie on the opposite sides of the line $3x-4y=8$, then

The perpendicular distance of the straight line $3x+4y=5\sqrt{5}$ from the origin is ______

Let $S$ be a subset of the plane defined by $S=\left\{\left(x,y\right):\left|x\right|+2\left|y\right|=1\right\}$. Then, the radius of the smallest circle with centre at the origin and having non-empty intersection with $S$ is

For the following shaded region, the linear constraints are 

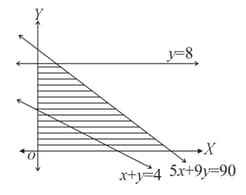
If one of the lines $2x^2-xy+b{y}^2=0$ passes through the point $\left(-4,-2\right),$ then $b^2=$

Consider the plane $x+y-z=1$ and point $A(1,2,-3)$ . A line $L$ has the equation $x=1+3r, y=2-r \& z=3+4r.$

 The distance between the points on the line which are at a distance of $4/\sqrt{3}$  from the plane is

A ray of light is projected from the origin at angle of $60°$ with the positive direction of $x$-axis towards the line, $y=2,$ which gets reflected from the point, $(\mathrm{\alpha },2).$ Then the distance of the reflected ray of light from the point $(2,2)$ is

The equation of the image of line $y=x$ with respect to the line mirror $2x-y=1$ is

The lengths of the perpendiculars from the points $\left(m^2,2m\right), \left(mn,m+n\right)$ and $\left(n^2,2n\right)$ to the line $x+\sqrt{3}y+3=0$ are in

Let $A(0, 1)$ and $B(2, 0)$, and $P$ be a point on the line $4x+3y=-9$.Then the coordinates of $P$ such that $\left|AP-PB\right|$ is maximum is:

The point $P(2,1)$ is shifted parallel to the line $x+y=1,$ by a distance of $5\sqrt{2}$ in the direction of increasing ordinate, to reach the point $Q.$ The image of $Q$ in the line $y=-x$ is

If the point $(a, a)$ falls between the lines $|x+y|=2,$ then :

Consider the points $A(3,4)$ and $B(7,13)$ If $P$ is a point on the line $y=x$ such that $PA+PB$ is minimum, then the coordinates of  $P$ are

The coordinates of the foot of the perpendicular from the point $(2,3)$ on the line $-y+3x+4=0$ are given by

A straight line through the origin $O$ meets the parallel lines $4x+2y=9$ and $2x+y+6=0$ at points $P$ and $Q,$ respectively. Then the point $O$ divides the segment $PQ$ in the ratio